Kepler's Laws of Planetary Motion
Navigate Astra's Guide to Orbits
Introduction > Kepler's Laws of Planetary Motion > Newton's Laws of Motion and Gravity > Spaceflight > Identifying Orbits > Lagrange Points > Orbital Elements > Orbit Terminology > Orbit Info and Resources

Johannes Kepler (1571-1630) was a mathematician and astronomer born in Weil der Stadt, Germany. Kepler's family was Lutheran and he wanted to be a clergyman, however mathematics, teaching, and astrology became his livelihood. He accepted the sun-centered solar system of Copernicus.
In 1600, Kepler joined the astronomer Tycho Brahe (1546–1601) in Prague to work as an assistant. Kepler used observations of the planet Mars made by Tycho Brahe to explain its motion. Tycho (1546–1601) himself did not believe in the Copernican theory, that was a problem for Kepler. Tycho insisted that Kepler must prove Tycho's own theory, where the Earth was the center of the universe, and the Sun and Moon revolved around it. According to Tycho, the other planets orbited the Sun.
After Tycho's death, Kepler managed to acquire the Mars data that he had been working on for Tycho. Kepler struggled to adapt the Mars observations to the geometrical equations set up by Copernicus or the system envisioned by Tycho. Observations of the planets showed that they were not moving in perfect circles or at constant speeds.
Kepler had already mastered two fundamental ideas that he published in his first astronomical work, Mysterium Cosmographicum or Cosmic Mystery. He believed that the Sun should be in the center of the system (not off center as Copernicus postulated), and speed of planets in their orbits should depend on their distance from the Sun.
Kepler's struggle to define the orbit of Mars became easier after he defined Earth's true orbit by plotting the Earth's position when Mars returned to the first position measured (using the star background or sidereal position.) He found that Earth's orbit wasn't a perfect circle after all! Most importantly, the Earth didn't travel at a constant speed. And last, by comparing the area that was swept out during a certain amount of time was equal to the area swept out at a different place in the orbit was equal!
One of the problems with Copernicus' helio-centric system was those darn circular orbits. Kepler made no progress until he accepted that God did not make the planets orbit in perfect circles. He kept trying to make the orbits into circles, after many years of frustration, he decided to try an oval. Although he wrote to a friend that he wished the orbits were ellipses, he didn't try to use this shape until he had exhausted the oval.
©2021 Dawn Jenkins
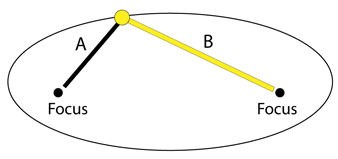
An ellipse is a shape that looks like a flattened circle. An ellipse is defined by two points, each one is a focus, and together are called, "foci". The sum of the distances to the foci from any point on the ellipse is always a constant. It is a closed curve formed by a set of points in a plane. As shown in figure 1, the sum of Distance A + Distance B is constant for any point on the curve of the ellipse.
An ellipse may be formed from the intersection of a circular cone and a plane cutting completely though the cone. The maximum diameter is called the "major axis." It determines the size of an ellipse. Half the maximum diameter, the distance from the center of the ellipse to one end, is called the "semi-major axis."
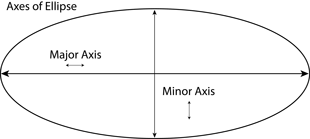
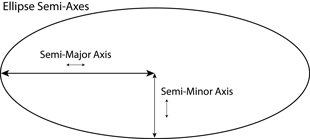
The longest distance across the ellipse is called the major axis, and it passes through the center of the ellipse. The shortest distance across the ellipse is called the minor axis, and it is perpendicular to the major axis at the center of the ellipse.
The shape of an ellipse is determined by how close together the foci are in relation to the major axis. Eccentricity is the distance between the foci divided by the major axis. If the foci coincide, the ellipse is a circle. Therefore, a circle is an ellipse with an eccentricity of zero. Eccentricity is an orbital element denoted by "e."
The illustration of the cone (figure 2) shows the various types of orbits that are common in the solar system, although none have been found that actually describe a true circle. The circle and the ellipse are closed orbits while the parabola and hyperbola are not closed. These orbits are usually associated with comets, the kind that whiz past the Sun and disappear forever when they leave the inner solar system.
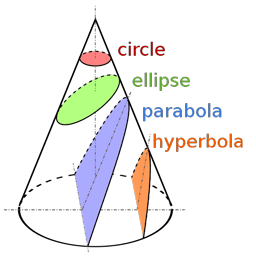
©Magister Mathematicae, CC 3.0
Kepler finally realized that the Mars' orbit was flattened on the sides. His pre-occupation with the planet Mars served him well, as Mars' orbit is more eccentric than most of the other planets. (The actual value of Mars' eccentricity "e" is 0.0934.) This is the reason why Mars' orbit always disagreed when measured against a circular orbit. A circular orbit just doesn't fit Mars' path in the sky.
After Kepler discovered the Earth moved at varying speeds in its orbit and Mars orbit described an ellipse, he was able to formulate his laws of planetary motion.

Kepler's laws of planetary motion are:
1. The orbit of every planet is an ellipse with the Sun at one of the two foci.
2. An imaginary line drawn from the center of the Sun to the center of an orbiting planet will sweep out equal areas during equal intervals of time.
3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
The first law may be called the "Law of Ellipses". It brought down the established idea that orbits were circular. Kepler's first law also shows that if a comet, or other object is observed to travel a hyperbolic path, it will visit the sun only once, unless it encounters a planet or other object that alters its trajectory.
Kepler's second law may be called the "Law of Equal Areas." It addresses the velocity of an object in orbit, and shows that the velocity along the path changes. With this law, it can be seen that a comet with a highly elliptical orbit has a velocity at closest approach to the Sun that is many times its velocity when farthest from the sun. The area of the orbital plane swept is still constant for any given period of time.

Kepler's third law, also called the "Law of Harmonies, describes the relationship between the masses of two objects revolving around each other and the determination of orbital parameters. Consider a small star in orbit about a more massive one. Both stars actually revolve about a common center of mass, which is called the "barycenter." This is true no matter what the size or mass of each of the objects involved. Measuring a star's motion about its barycenter with a massive planet is one method that has been used to discover planetary systems associated with distant stars. These statements apply to a two-dimensional picture of planetary motion, that is what is needed for describing orbits. A three-dimensional picture of motion would include the path of the Sun through space.
Continue following through Astra's Orbit Guide by moving on to Newton's Laws of Motion and Gravity
#AstrasStargate #ImaRocketFan

This webpage is ©2023 D. E. Jenkins all rights reserved. Please use the contact page to get permission to use this content or to send comments or corrections.
Navigate Astra's Guide to Orbits - or return to Orbits home
