On this page: Copernicus > Planet Orbits and Retrograde Motion also find here -
Overview of Orbit Guide Topics: Kepler's Laws > Newton's Laws and Gravity > Spaceflight > Lagrange Points
Introduction
Understanding orbits is important astronomically and for space exploration. In astronomy, orbits are the fundamental movement of all the stars and planets. This is known as celestial mechanics. They are important for space exploration because objects in space must follow curved paths. Orbital mechanics is also called astrodynamics, that is, using ballistics and celestial mechanics to describe the motion of rockets and spacecraft.
Historically, humans had to solve the mysteries of the planets. Why did they move among the stars and change their brightness? The orbit of the Moon around the Earth and the Earth around the Sun had to be "discovered" because it is not obvious to individuals living on the surface of the Earth. Why did the phases of the Moon seem so regular, but why did it appear so late at times? Popular thought was that the Earth was the center of the universe. Planetary motions were confusing because sometimes they retraced their steps moving backward from their normal motion. Complex schemes were developed to explain how this worked in the Earth-centered system.
This orbit series at Astra's Stargate will trace the history of the astronomical advances that brought humans from wondering why things fall to launching giant rockets into the sky and landing spacecraft at targeted planets that are millions of miles away. Discover how we went from planetary orbits to rocket trajectories in just four centuries.
We will explore the types of orbits that are used to place satellites into the proper orbit to carry out the missions that are assigned to them. We will look at various orbits, those based around Earth, others used by comets and asteroids, as well as the orbits used by interplanetary space missions.
To skip the historical overview, continue to the main page of Kepler or Newton. This page contains detailed information pre-Kepler and overviews of guide topics.
In the 9th century the old Greek knowledge had been translated and was accepted by the Church. The scheme developed by Ptolemy to explain the motion of the planets and Sun about the Earth was generally accepted. In this scheme, Ptolemy (100-170 AD) introduced epicycles to describe the motions. In this system, planets moved in circular orbits around a circle called a "deferent". This explained retrograde motion but required 40 epicycles to explain the Earth-centered system. The source of this knowledge came in the form of Ptolemy's work, "The Almagast", one of the earliest astronomical books. Soon, church authorities became intolerant of any diversion from Ptolemy.
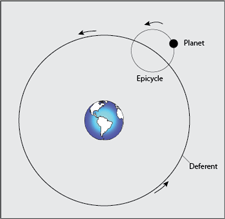
fit circular orbit models
It was Nicholas Copernicus (1473-1543) who put forth the theory that the Sun was the central body and that Earth and the other known planets orbited the Sun. Because this was a revolutionary theory in its time, Copernicus did not publish until 1543, just two months before he died. His masterwork was entitled, "De revolutionibus orbium coelestium" or "On the Revolutions of the Celestial Spheres". Today we recognize the solar system, a term that describes the systematic motions of the planets under the Sun's rule. Copernicus introduced a "heliocentric" system. Using the observations available in his time, Copernicus was able to calculate the approximate distance of each planet's orbit from the Sun. In his system he made seven assumptions (called "axioms" here.)
Copernicus' Axioms
1. There is no one center of all the celestial circles or spheres.
2. The Earth's center is not the center of the universe, only of gravity and the Moon.
3. All the spheres revolve around the Sun as the midpoint of their orbit, therefore, the center of the universe is near the sun.
4. The distance from the Earth to the Sun is imperceptible compared with the distance to the stars.
5. The rotation of the Earth accounts for the apparent daily rotation of the stars.
6. The apparent annual cycle of movements of the sun is caused by the Earth revolving round it. This means the Earth has more than one motion.
7. The apparent retrograde motion of the planets is caused by the motion of the Earth, our observing platform.
In the Copernican System, the Earth was nothing more than a planet in the solar system, not the divine home of humans around which everything revolved. Earth is moving constantly, even though that motion can not be felt. Under Copernicus the Earth has three motions, its daily rotation, annual revolution, and annual tilting of its axis (today we know the axis changes very slowly.) The distance from the Earth to the Sun is small compared to the distance to the stars, and the center of the universe is near the Sun. Unfortunately, Copernicus envisioned the planets as moving in a circular orbit, but observational techniques even in that day proved that they are not. Heavenly motions are uniform, eternal, and circular or made of several circles (epicycles).
Copernicus' heliocentric cosmology established Mercury and Venus as "inner planets", that is they are on the inside of Earth's orbit of the Sun. Planets that orbit outside of the Earth's orbit are called "outer" planets. Other terms for inner and outer planets are "inferior" and "superior" planets.
Copernicus was careful to use sidereal observations of planets as opposed to synodic. The "synodic period" is the time that lapses between two identical positions of Earth and another body such as the Moon. For example, the Moon's synodic period is from New Moon to New Moon. The "sidereal period" is when an object returns to an identical position in the sky against the star background.
Planets Orbits and Retrograde Motion
After Copernicus the peculiar backward motion of the planets could be solved. As the planets go about their orbits, Mars appears to move through the constellations on the ecliptic in a regular pattern from West to East as viewed from Earth. This is contrary to the motion of the stars that move from East to West as the Earth rotates. This is called prograde motion. At first Mars seems to behave as usual, but then it pauses, and starts to move in the opposite direction or retrograde motion.
Before retrograde motion begins, Mars or other outer planets seem to stand still. This can be thought of as Earth, coming around the curve of its orbit so that Mars appears to quit moving. This is merely our line-of-sight. It's like being on a train when it is being passed by a faster train. If you are looking at the train out the window, suddenly you feel like you are moving backwards. Earth and Mars are doing something like this, the blue planet is lapping the red planet on their orbital tracks. After that it appears to travel in a backward direction (East to West) until after opposition when it hits another stationary point. Then it resumes its normal course, although it really did nothing but continue to maintain its usual orbit. It is only our line-of-sight that makes Mars and other outer planets seem to move in a loop or sometimes an ess-curve against the background stars.
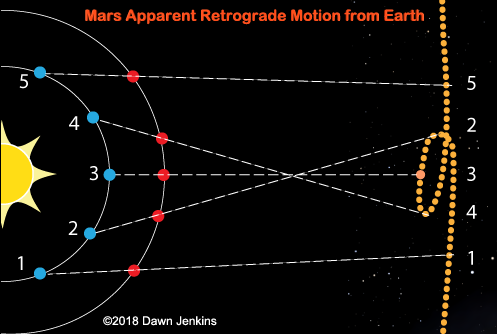
The diagram below shows how this works. Earth's position is marked in blue and the Mars position is marked in red. An observer on the Earth looks at Mars when they are located at position 1. The Earthling sees Mars against the star background moving in its usual prograde motion from west to east. A short while later both Earth and Mars arrive at the position 2, Mars appears to stand still and retrace its steps. At position 3, the observer is treated to the happy circumstance of Mars at opposition. The Sun is behind the Earth, the disk of Mars or other outer planet will be 100% illuminated. At position 4, the Earth observer sees that Mars is stopping and returning to its normal contrary motion moving from west to east against the background field of stars. At position 5, Mars has been left behind and both planets orbit the Sun until their mutual speeds and positions reunite them for the next opposition.
Copernicus lived during the Renaissance, a period of rebirth in arts, science and culture in Europe. Even so, Copernicus' theory was not universally accepted by authorities of the day, and powerful institutions resisted the notion. Orbital mechanics were still a mystery to be unraveled. There was a major force at play that we know today: Gravity.
To understand planetary motion and orbits, the force of gravity also had to be understood. Church authorities found another irrefutable Greek scientist in the person of Aristotle. In Aristotle's view, gravity made bodies move towards their natural place when no force is acting on them. Today we know that bodies that are not in motion have inertia and once they are forced to move, they will continue moving in the same direction at that speed until another force acts upon them. Aristotle said that the speed of two identically shaped objects placed in water will sink or fall directly proportional to their weights and inversely proportional to the density of the medium through which they move. Although today we know the medium can make a big difference, weight is not a factor in the rate that they fall. Scientists had to go up against the Church as well as popular belief to change the views that were being held as irrefutable. This was no trivial matter as the Church was powerful, this impacted scientific thought and written works.
One pioneer was Galileo Galilei (1564-1642) who conducted gravity studies. Galileo dropped balls constructed of the same material, but different masses demonstrating that the object's time of descent was independent of its mass. Galileo also was among the first to use the newly invented telescope to spot the moons of Jupiter orbiting the planet and the planet Venus exhibiting "phases." His work went far to validate the basic Copernican theory but unfortunately made him a criminal in the eyes of the Church. Elsewhere in Europe, Johannes Kepler (1571-1630) was formulating laws for planetary motion.

Kepler's Law of Planetary Motion
Johannes Kepler (1571-1630) was a mathematician and astronomer born in Weil der Stadt, Germany. Kepler accepted the sun-centered solar system of Copernicus. In 1600, Kepler joined the astronomer Tycho Brahe (1546–1601) in Prague to work as an assistant. Kepler used observations of the planet Mars made by Tycho Brahe (a keen observer before the age of the telescope) to explain its motion. Tycho himself did not believe in the Copernican theory and he insisted that Kepler must prove Tycho's own theory, where the Earth was the center of the universe, and the Sun and Moon revolved around it.
Kepler's laws of planetary motion are:
1. The orbit of every planet is an ellipse with the Sun at one of the two foci.
2. An imaginary line drawn from the center of the Sun to the center of an orbiting planet, will sweep out equal areas during equal intervals of time.
3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
The first law may be called the "Law of Ellipses". as it brought down the established idea that orbits were circular. Kepler's second law may be called the "Law of Equal Areas." Kepler's third law, also called the "Law of Harmonies, it describes the relationship between the masses of two objects revolving around each other and the determination of orbital parameters.
These are the summarized Kepler's laws of planetary motion, for more in-depth information use the Kepler's Laws page

Newton's Laws and Gravity
Building on Kepler's planetary laws, Newton was able to explain gravity and how it worked to keep objects in orbit. To help in understanding how gravity worked, Newton developed an interesting thought experiment that we know today as Newton's Cannon. Here is an overview of the laws Newton developed; continue to the Newton's Laws and Gravity page to study these topics in depth.
First Law : Inertia
An object at rest will remain at rest, and an object in motion remains in motion at constant speed and in a straight line unless it is compelled to change its state by the action of an external force.
Second law : Force
The acceleration of an object is directly proportional to the net force applied to it and inversely proportional to the mass of the object.
Third Law : Action and Reaction
When one object exerts a force on a second object, the second object exerts an equal and opposite force on the first.
Achieving Spaceflight
Find out on Newton's page how the laws of motion and our knowledge of orbital mechanics helped to understand what is necessary to keep satellites in place near the Earth, enabled humans to travel to the Moon, and send out probes to every planet in the solar system. Newton also developed the Universal Gravitation law that explains how gravity works.
Newton’s Law of Universal Gravitation
The force of gravity between two bodies is directly proportional to the product of their two masses and inversely proportional to the square of the distance between them.
This page presents a mere summary of Newton's Laws of Motion, find out more on the Newton's Mechanics and Gravity page. There you will find the details and learn about Newton's Cannon and achieving spaceflight. Or, go directly to the Spaceflight page.

Classifying Orbits
In the many years that humans have been launching satellites and spacecraft from the Earth, many types of orbits have been calculated and used for a variety of purposes. Orbits have to be defined and therefore they have been classified. There are many different categories of orbit that have been used since the early days of the space age. For now, this section contains very basic information covering some of the various types of orbit. Stay tuned for the orbital classification pages coming to Astra's Guide to Orbits.
Types of Orbits
Orbits can be centric, that means they are defined by the body that an object is orbiting. That may be a star, a planet, or another body in the solar system. The more massive body is referred to as the "primary." The most commonly used centric orbits are based on the Earth as the primary body. Orbiting satellites are used for communications, navigation, Earth observation, and other purposes. These are "geocentric" or Earth orbits and are broken down by altitude.
Geocentric Orbits by Altitude
Low Earth Orbit (LEO) - altitudes 62 miles or 100 km, to 1,240 miles or 2,000 km
Medium Earth orbit (MEO) - altitudes 1,240 miles or 2,000 km to 22,236 miles or 35,786 kilometers
High Earth orbit - altitudes from 22,240 miles or 35,786 km
Orbits can be classified by inclination. The orbit is measured by the tilt of the objects orbit around the primary body. Typical inclined orbits are polar and equatorial.
Orbits are also identified by their eccentricity. These are circular or elliptic orbits. In a circular orbit the eccentricity is zero, but elliptical orbits have an eccentricity that is greater than zero but less than one.
Another classification is synchronicity, that means occurring at the same time. Synchronous orbits have a relationship that is in some way time based. Perhaps the best known is the Geosynchronous orbits (GEO), a high orbit (22,236 miles or 35,786 km) where a satellite can be placed so that it remains stationary over a location on the planet.
Orbits can be reckoned by their period. Planets in the solar system are often defined by their period. The Earth's orbit has the familiar period of 365.256 days, that is a sidereal year.
Other orbits called transfer orbits are used to take spacecraft to other planets. The most used orbit of this kind is the Hohmann transfer orbit. It is used over other orbits because it can save fuel. Hohmann transfer orbits start out in low-earth orbit, then perform burns that place the spacecraft in an orbit that intersects with the orbit of the destination planet.
- - Orbit classification will be discussed in depth on a new page at Astra's in the future.

Orbital Elements
To describe an orbit mathematically, there are six quantities that must be known. These quantities are called orbital elements, or Keplerian elements, after Johannes Kepler who defined them:
- Eccentricity (e)
- Semi-major axis (a)
- Inclination (i)
- Argument of periapsis (ω)
- Time of periapsis passage (T)
- Longitude of the ascending node (Ω)
- - These quantities will be discussed in depth on the orbital element page at Astra's in the future.
Lagrange Points
Joseph Louis Lagrange (1736-1813) showed how a body of small mass could orbit along with a more massive body that is already in a near-circular orbit around another body. In a frame of reference that rotates with the more massive bodies, he found five points where the combined gravitational forces of the two larger bodies can keep the small mass rotating in a constant relative position as they orbit. There are five Lagrange points around two major bodies like a planet or a star. Spacecraft may utilize lagrange points using a special orbit called a "halo orbit." Lagrange wrote about these points in a 1772 paper, that is called the "three-body problem."
A Lagrange point or libration point is a location in space where the combined gravitational forces of two large celestial bodies balance or equal the centrifugal force felt by a much smaller third body. The interaction of the forces creates a point of equilibrium where an asteroid may take up a stable orbit or a spacecraft can linger to make observations.
This subject will be discussed in more detail on a future orbit page at Astra's. In addition, the special halo orbit that is to be used by the planned Gateway space station is presented on the Lunar Gateway page at Astra's.
Continue following through Astra's Orbit Guide by moving on to Kepler's Laws of Planetary Motion

#AstrasStargate #ImaRocketFan
This webpage is ©2023 D. E. Jenkins all rights reserved. Please use the contact page to get permission to use this content or to send comments or corrections.
Navigate Astra's Guide to Orbits - or return to Orbits home
