Newton's Laws and Gravity

While Kepler's Laws presented the solutions to some of the questions left by the heliocentric model of the solar system, it still remained to explain one of the main components that enabled the motion, gravity. It was the 17th century mathematician, Isaac Newton (1642-1727) that defined his laws of motion and formulated his law of universal gravitation.
Sir Isaac Newton realized that the force that caused apples fall to the ground is the same force that caused the planets to "fall" around the sun. Newton developed the law of universal gravitation that states every particle attracts every other particle in the universe. He established that a force of attraction toward the sun becomes weaker in proportion to the square of the distance from the sun. This is called, the "inverse-square law".
Navigate Astra's Guide to Orbits
Introduction > Kepler's Laws of Planetary Motion > Newton's Laws of Motion and Gravity > Spaceflight > Identifying Orbits > Lagrange Points > Orbital Elements > Orbit Terminology > Orbit Info and Resources
Newton’s work accepts that the planets move around the Sun in orbits shaped as ellipses. Circular orbits are merely a special case of an ellipse where the foci coincide (any point on the circle is the same distance from the center). Newton described his work in the "Principia Mathematica Philosophiae Naturalis" (in English, Mathematical Principles of Natural Philosophy) often called simply the "Principia", that he published in 1685. Thus, Isaac Newton originated the field of orbital mechanics.
Newton's Laws of Motion
First Law : Inertia
An object at rest will remain at rest, and an object in motion remains in motion at constant speed and in a straight line unless it is compelled to change its state by the action of an external force.
The first law is the actual definition of inertia. It was Galileo Galilei who defined inertia, stating if there is no net force acting on an object (net means all the external forces cancel each other out), then the object will maintain a constant velocity. If the velocity is zero, then the object remains at rest. If an external force is applied, the velocity will be changed because of that additional force.
Second law : Force
The acceleration of an object is directly proportional to the net force applied to it and inversely proportional to the mass of the object.
This may well be the most important law of physics and is mathematically expressed as: F = ma . It applies to a body with a constant mass (m), where F means force and a means acceleration.
If a body has a net force acting on it, it is accelerated as described by the equation. Conversely, if a body is not accelerated, there is no net force acting on it. Acceleration, velocity, momentum and force are vector quantities. There are three ways to modify the momentum of a body. The mass can be changed; the velocity can be changed (acceleration), or both.
Acceleration may be produced by applying a force to a mass (such as a spacecraft). If applied in the same direction as an object's velocity, its velocity increases in relation to an un-accelerated observer. If acceleration is produced by applying a force in the opposite direction from the object's original velocity, it will slow down relative to an un-accelerated observer. If the acceleration is produced by a force at some other angle to the trajectory, the object will be deflected.
Acceleration in Orbit
Newton's first law describes how, once in motion, planets remain in motion. What it does not do is explain how the planets are observed to move in nearly circular orbits rather than straight lines. This is explained by the second law. To move in a curved path, a planet must have acceleration toward the center of the circle. This is called, "centripetal acceleration" and is supplied by the mutual gravitational attraction between the sun and the planet. (Centripetal means center-seeking force.)
Third Law : Action and Reaction
When one object exerts a force on a second object, the second object exerts an equal and opposite force on the first.
In other words, for every action, there is an equal and opposite reaction.

Newton's Cannon - Obtaining an Orbit
To illustrate the physics of orbital mechanics, Isaac Newton developed a thought experiment using a fictitious cannon mounted on top of a mountain. By using more and more gunpowder, the cannonball would be able to attain greater and greater speeds, until there is enough energy to "launch" the cannonball off the surface of the Earth. This thought experiment is known as "Newton’s Cannon" or Cannonball, and also "Newton’s Mountain." It was published by Isaac Newton in the Principia and translated into English in 1728, "A Treatise of the System of the World". It included the familiar drawing of the cannon that is widely used to illustrate it. (Hint: the treatise can be downloaded from Google Books.)
It is a thought experiment intended to illustrate the important points, so some facts must be ignored. Of course, it is impossible to have such a high mountain on Earth and the drag caused by the Earth's atmosphere on the cannonball must be ignored. A typical cannon cannot provide enough energy to lift the projectile so high. Nor does it consider the Earth's rotation. It is an experiment intended to illustrate orbital mechanics and help us to understand the principles of orbital mechanics.
A. If a cannon fires its cannonball with low initial speed, the trajectory of a ball curves downward, falling as a result of Earth's gravity, and hits the ground.
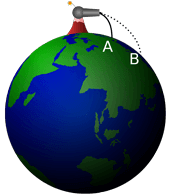
B. By packing more gunpowder into the cannon, the next time it's fired, the cannonball goes faster, but still curves downward and this time travels farther, but it is falling to Earth and hits the ground. The path of the cannonball is a ballistic arc.
C. Packing still MORE gunpowder into Newton's cannon, the cannonball will travel much faster, and so much farther that it never has a chance to touch the ground. The ground curves away from the cannonball at least as much as the cannonball falls – so that the cannonball never hits the ground. It is falling completely around Earth! Now we can say it has achieved orbit.
This is how a spacecraft achieves orbit. First it gets a strong boost from a rocket, and then it simply continues to fall - - for the rest of its orbital life. Modern spacecraft are not cannonballs, and they are equipped with small thrusters that allow them to make adjustments in orbit. Without additional rocket engine burns, they continue falling.

Does Not Touch the Ground
For any specific combination of height above the center of gravity and mass of the Earth, there is one specific firing speed (that is unaffected by the mass of the ball, because it is assumed to be very small relative to the Earth's mass) that produces a circular orbit as shown in figure C.
This same principle can demonstrated by using an ordinary ball. When you throw the ball in front of you with little speed, it falls to the ground. As you throw it faster and faster, it travels further but still it eventually falls to the ground. If you could throw the ball at 17,500 mph (28,800 km/h), it would continue to fall around the Earth. This is the speed of the International Space Station as it orbits the Earth. It is at the right height of ~248 miles or 400 kilometers and traveling at the right speed that enables it to stay in orbit while its falling around the Earth.
In its elliptical orbit, part of the orbit comes closer to Earth’s surface than the rest of it does, it is called the periapsis of the orbit. Before the cannonball is launched, the mountain represents the highest point in the orbit. That's called the apoapsis. The altitude affects the time it takes to complete an orbit is called the orbital period. The period of the International Space Station, at ~248 miles or 400 kilometers, is 90 minutes.
D. As the speed of the cannonball is still increased, the cannonball can achieve an elliptical orbit. If the initial firing is above the surface of the Earth as shown, there will also be non-interrupted elliptical orbits at slower firing speed; these will come closest to the Earth at the point half an orbit beyond, and directly opposite the firing point, below the circular orbit.
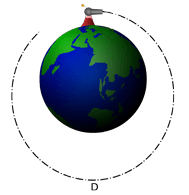
the Cannonball can Reach Orbit
E. Finally, at a specific firing speed called, "escape velocity", that is dependent on the mass of the planet; an open orbit is achieved that has a parabolic path. At even greater speeds the object will follow a range of hyperbolic trajectories. In a practical sense, both of these trajectory types mean the object is "breaking free" of the planet's gravity, and "going off into space" never to return.
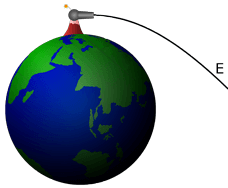
Escape Velocity Leaves Earth
- - find simulations of Newton's Cannon online on Astra's Orbit Info and Resources
Newton’s Law of Universal Gravitation
The force of gravity between two bodies is directly proportional to the product of their two masses and inversely proportional to the square of the distance between them.
Newton knew that gravity caused objects to be attracted to the Earth, and he was able to measure the affect of Earth's gravity on the Moon. This law is very important in astronomy and spaceflight, because it can be used for all objects in the universe with respect to each other. The force of gravitational attraction, is directly dependent upon the masses of both objects and inversely proportional to the square of the distance that separates their center of mass.
For orbits, universal gravity is an important force that must be taken into consideration. Gravity is the force that makes orbit possible. For practical purposes, the mass of the Earth and the mass of spacecraft and satellite and the distance between them, are crucial in determining orbits.

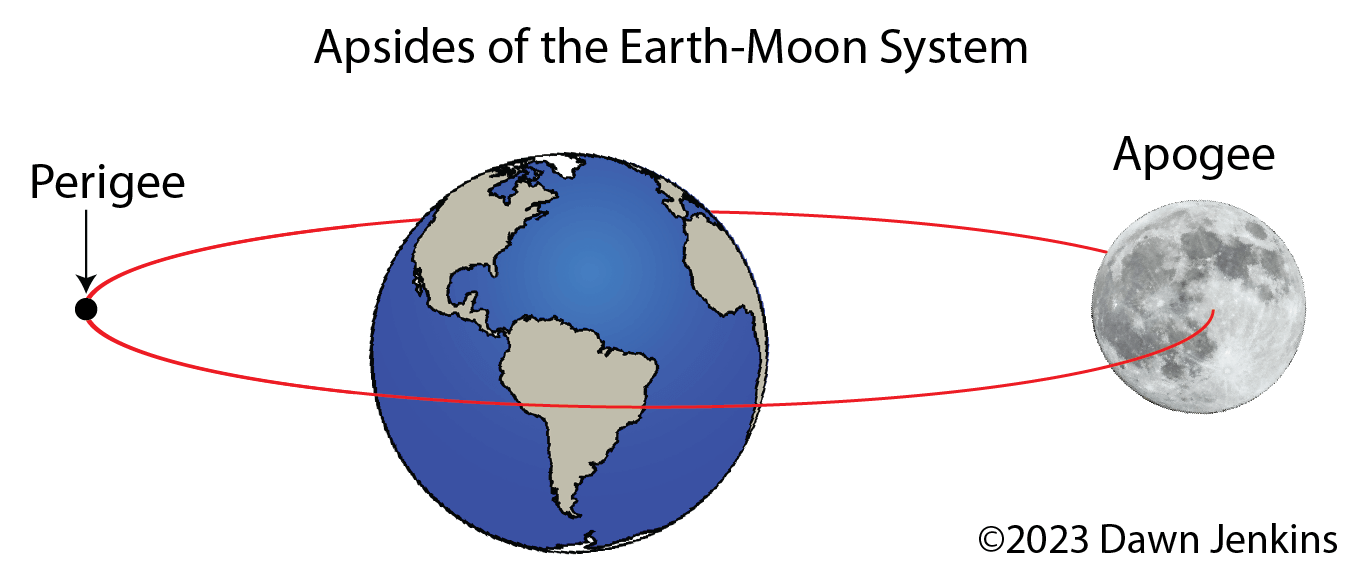
The Apsides of an Elliptical Orbit
When Newton's cannonball was fired at a speed fast enough to orbit the Earth, two orbital parameters were introduced. These are important terms for an elliptical orbit, for in this orbit the two bodies orbit around a common center. The smaller body travels in an elliptical path that brings it closer to the parent body or further. These two different positions in the orbit are called, "apsides". The line connecting the two extreme points of the orbit is called, "the line of apsides". The terms "periapsis" and "apoapsis" were first used by Johannes Kepler.
Apoapsis
Apoapsis is the point at which an orbiting object is farthest away from the body it is orbiting. This point is sometimes given a name that is specific to the body being orbited. For example, the apoapsis of an object orbiting Earth is its apogee (from Gaia, the Greek word for Earth), and the apoapsis of an object orbiting the Sun is called, "aphelion" (from helios, the Greek word for Sun). According to Kepler's laws of planetary motion, an object is at its lowest velocity at the apoapsis.
Periapsis
Periapsis is the point at which an orbiting object is closest to the body it is orbiting. This point also is sometimes given a name that is specific to the body being orbited. For example, the periapsis of an object orbiting Earth is its perigee. According to Kepler's laws of planetary motion, an object is at its greatest velocity at the periapsis.



Isaac Newton defined laws that would help humans get into space, although it would take a few centuries before the first rocket put a spacecraft into outer space. Incidently, the edge of space from Earth is defined today as the Karmen line, named after aerospace engineer, Theodore von Kármán who first proposed the boundary between the Earth's atmosphere and space as 62 miles or 100 kilometers.
Continue following through Astra's Orbit Guide by moving on to Spaceflight
#AstrasStargate #ImaRocketFan
This webpage is ©2023 D. E. Jenkins all rights reserved. Please use the contact page to get permission to use this content or to send comments or corrections. Newton's Cannon images from Wikimedia Commons were originally created by Brian Brondel, have been adapted for Astra's Stargate and are posted here with CC3.0 license.
Navigate Astra's Guide to Orbits - or return to Orbits home
